Singular Value Decomposition (SVD) using MATLAB

MATLAB Programs:

% Singular Value Decomposition (SVD)

 A=[4 2 3; 3 -5 2; -2 3 8];    % Square matrix A

 B=[4 2 3 8; 3 -5 2 -14; -2 3 8 27];  % Rectangular matrix B

 fprintf('SVD for the matrix A: \n');

 [U, S, V]=svd(A)

 fprintf('\n\nSVD for the matrix B: \n');

 [U, S, V]=svd(B)

OUTPUTS:

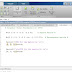
>> svd_code

SVD for the matrix A: 

U =

    0.3572    0.3823   -0.8522

   -0.0380    0.9176    0.3957

    0.9332   -0.1090    0.3423

S =

    9.2534         0         0

         0    6.4751         0

         0         0    4.0556

V =

   -0.0596    0.6950   -0.7166

    0.4003   -0.6410   -0.6549

    0.9144    0.3259    0.2400

SVD for the matrix B: 

U =

   -0.2574   -0.4506   -0.8548

    0.4300   -0.8456    0.3163

   -0.8654   -0.2862    0.4114

S =

   32.6661         0         0         0

         0    6.9982         0         0

         0         0    4.1169         0

V =

    0.0610   -0.5383   -0.7999    0.2582

   -0.1610    0.3527   -0.4996   -0.7746

   -0.2092   -0.7620    0.3301   -0.5164

   -0.9626    0.0725   -0.0388    0.2582